Difference between revisions of "Compensation of distortion"

Latest revision as of 17:29, 30 July 2013

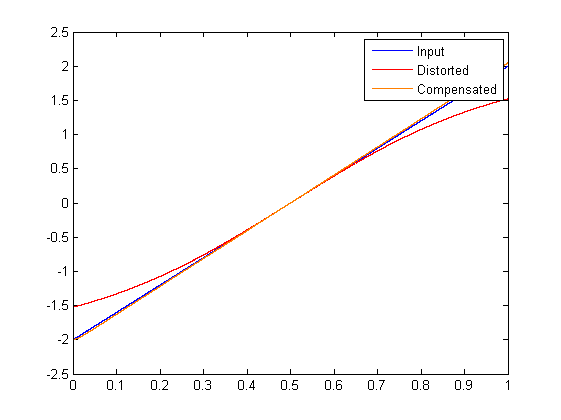
Many electronic systems exhibit some degree of nonlinearity. While this is acceptable to some degree, pushing a device deep into saturation will drastically reduce the utility of one's collected data. We have developed a technique to automatically remove this distortion without knowledge of the distorting transfer function, by stretching regions of the output so that the noise floor remains constant over the entire output range.

We have implemented this technique using both Matlab and Labview, and have made our software available at https://github.com/LachlanGunn/stochastic-instrumentation-tools.

First, a brief example:

t = 0:0.2e-5:1;
        
% Make a ramp.
input = (t-0.5)*4 + 1e-4*randn(size(t));
 
% Distort the ramp with a logistic function.
distorted =  ( 1./(1+exp(-input)) - 0.5 )*4;
 
% Undo the distortion.
est_input = compensate_nonlinear(distorted , 40, 1e-3);
 
% Plot the results
figure();
plot(t, input, 'b');
hold on;
plot(t, distorted, 'r');
plot(t, est_input, 'Color', [1, 0.5, 0]);
hold off;
legend('Input', 'Distorted', 'Compensated');

We see that compensate_nonlinear has been able to recognise the shape of the distortion and remove its effect.