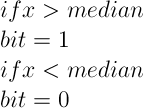Timing-based key agreement: Difference between revisions
m Created page with '=Timing Based Key Agreement Protocol= A paper from Maurer & Gander , ‘On the Secret-Key Rate of Binary Variables’, which expanded on Claude Shannon’s work revealed to us w...' |
mNo edit summary |
||
| Line 1: | Line 1: | ||
=Timing Based Key Agreement Protocol= | =Timing Based Key Agreement Protocol= | ||
==Introduction== | |||
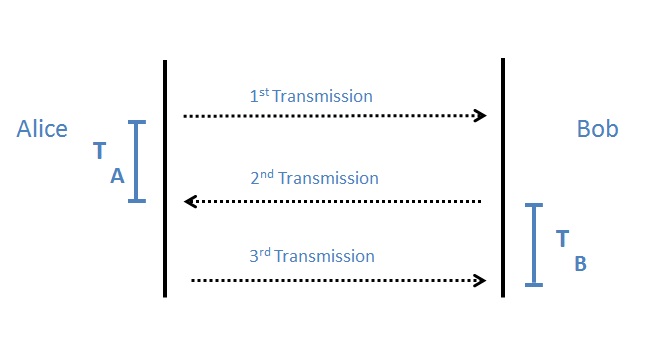
A paper from Maurer & Gander , ‘On the Secret-Key Rate of Binary Variables’, which expanded on Claude Shannon’s work revealed to us when the encryption operators used by Bob and Alice are independent – the secrecy rate is zero. | A paper from Maurer & Gander , ‘On the Secret-Key Rate of Binary Variables’, which expanded on Claude Shannon’s work revealed to us when the encryption operators used by Bob and Alice are independent – the secrecy rate is zero. A new approach was take in the project - as the previous method of attempting to do two independent rotations would clearly not work. This new method was using the round trip times between the sender and recipient as the way to generate a key. The round trip times are generated as shown in the image below. | ||
[[File:RoundTripTimes.jpg]] | |||
Once the round trip times are generated, they are turned into a bit stream by using the formula shown. | |||
[[File:MedianEq.png]] | |||
Due to the fact that the internet is not a perfect communication channel, the round trip times observed by the sender and recipient are going to be different - hence the bit streams generated are going to be different. Therefore, as of yet we cannot use these as a secure key. If we consider the situation from an eavesdropper, say Eve's, perspective, we notice that while Alice and Bob are able to communicate and directly generate their respective round trip times, Eve is only able to estimate the round trip times. Due to the randomness of the internet, and any further timing delays which occur when the packets actually reach the sender/recipient, Eve will never have the same quality of information as the Alice and Bob. | |||
[[File:RTT_E.png]] | |||
The next step is to reconcile Bob and Alice's bit streams - but do this in such a way that we further extend our advantage over Eve. This is done through a process called advantage distillation, and our chosen advantage distillation protocol was called the bit pair iteration protocol. During this process, Alice and Bob directly communicate with each other, and through parity checks determine which bits are correct or incorrect. | |||
Consider Eve, if is in the channel eavesdropping as shown in the diagram above, when the bit pair iteration protocol takes place, she is able to eavesdrop on which packets are deemed as being incorrect by Alice and Bob. However, even though these packets are incorrect for Alice and Bob, if we recall the fact that due to the randomness that all of the bit streams will be different, there is no guarantee that they are incorrect for her. This can result in her keeping incorrect bits, and discarding correct bits. Therefore, in theory, Eve's bit error rate should not drop as quickly as Bob and Alice's bit error rate. An example is shown below. | |||
Imagine the three bit streams below are obtained: | |||
Alice: 11001001 | |||
Bob: 01101001 | |||
Eve: 10000111 | |||
Say Alice and Bob perform Bit Parity Checks - we notice that the first and second bit pairs will be thrown out due to the parity check failing | |||
Now if we imagine Eve is listening to these Bit Parity Checks - she would respond by throwing out the first and second bit pairs. | |||
However, in Eve's case - the first and second bit pairs would have been consistent. | |||
Alice Reconciled Bit Stream: 10 | |||
Bob Reconciled Bit Stream: 10 | |||
Eve Reconciled Bit Stream: 01 | |||
In this case, the bit error rate between Bob and Alice is 0 % | |||
Meanwhile, the bit error rate between Eve and Alice is 100 % | |||
Revision as of 09:11, 24 October 2013
Timing Based Key Agreement Protocol
Introduction
A paper from Maurer & Gander , ‘On the Secret-Key Rate of Binary Variables’, which expanded on Claude Shannon’s work revealed to us when the encryption operators used by Bob and Alice are independent – the secrecy rate is zero. A new approach was take in the project - as the previous method of attempting to do two independent rotations would clearly not work. This new method was using the round trip times between the sender and recipient as the way to generate a key. The round trip times are generated as shown in the image below.
Once the round trip times are generated, they are turned into a bit stream by using the formula shown.
Due to the fact that the internet is not a perfect communication channel, the round trip times observed by the sender and recipient are going to be different - hence the bit streams generated are going to be different. Therefore, as of yet we cannot use these as a secure key. If we consider the situation from an eavesdropper, say Eve's, perspective, we notice that while Alice and Bob are able to communicate and directly generate their respective round trip times, Eve is only able to estimate the round trip times. Due to the randomness of the internet, and any further timing delays which occur when the packets actually reach the sender/recipient, Eve will never have the same quality of information as the Alice and Bob.
The next step is to reconcile Bob and Alice's bit streams - but do this in such a way that we further extend our advantage over Eve. This is done through a process called advantage distillation, and our chosen advantage distillation protocol was called the bit pair iteration protocol. During this process, Alice and Bob directly communicate with each other, and through parity checks determine which bits are correct or incorrect. Consider Eve, if is in the channel eavesdropping as shown in the diagram above, when the bit pair iteration protocol takes place, she is able to eavesdrop on which packets are deemed as being incorrect by Alice and Bob. However, even though these packets are incorrect for Alice and Bob, if we recall the fact that due to the randomness that all of the bit streams will be different, there is no guarantee that they are incorrect for her. This can result in her keeping incorrect bits, and discarding correct bits. Therefore, in theory, Eve's bit error rate should not drop as quickly as Bob and Alice's bit error rate. An example is shown below.
Imagine the three bit streams below are obtained: Alice: 11001001 Bob: 01101001 Eve: 10000111 Say Alice and Bob perform Bit Parity Checks - we notice that the first and second bit pairs will be thrown out due to the parity check failing Now if we imagine Eve is listening to these Bit Parity Checks - she would respond by throwing out the first and second bit pairs. However, in Eve's case - the first and second bit pairs would have been consistent.
Alice Reconciled Bit Stream: 10 Bob Reconciled Bit Stream: 10 Eve Reconciled Bit Stream: 01
In this case, the bit error rate between Bob and Alice is 0 % Meanwhile, the bit error rate between Eve and Alice is 100 %