Geometric algebra: Difference between revisions
| Line 12: | Line 12: | ||
===What is GA?=== | ===What is GA?=== | ||
Geometric Algebra is the Clifford Algebra of a vector space over the field of real numbers endowed with a quadratic form. It's an elegant mathematical framework for expressing geometrical ideas and doing computations in fields such as physics, engineering and in computer vision (see [https://www.eleceng.adelaide.edu.au/personal/dabbott/wiki/index.php/Semester_B_Final_Report_2013_-_Secure_communications_without_key_exchange%3F_2013#Geometric_Algebra Final Report GA] for a list of some research applications). It correctly expresses the properties of physical space and one of the main benefits for our project was that it could be extended effortlessly to spaces of arbitrary dimensions. | Geometric Algebra is the Clifford Algebra of a vector space over the field of real numbers endowed with a quadratic form. It's an elegant mathematical framework for expressing geometrical ideas and doing computations in fields such as physics, engineering and in computer vision (see [https://www.eleceng.adelaide.edu.au/personal/dabbott/wiki/index.php/Semester_B_Final_Report_2013_-_Secure_communications_without_key_exchange%3F_2013#Geometric_Algebra Final Report GA] for a list of some research applications). It correctly expresses the properties of physical space and one of the main benefits for our project was that it could be extended effortlessly to spaces of arbitrary dimensions. | ||
[[Image:DefiningVectors.jpg|left|750px]] | [[Image:DefiningVectors.jpg|left|750px]] | ||
====Defining Vectors==== | |||
==How we used it?== | ==How we used it?== | ||
Revision as of 10:13, 28 October 2013
Rationale
As the main approach inherent in this project involved the use of rotations in Geometric Algebra, we were required to learn the basics of GA with the help of Dr James Chapel. The following description/brief introduction to the fundamental elements of GA is a combination of James' two documents below and numerous other sources. James graciously provided us with his personal powerpoint slides that proved to be an invaluable resource in learning the new materiala as well as a brief worksheet to test your knowledge on GA. Both are provided below.
Intro to Clifford's Geometric Algebra & Worksheet #1 in Geometric Algebra
"...it is a good thing to have two ways of looking at a subject, and to admit that there are two ways of looking at it.” James Clerk Maxwell
Geometric Algebra Intro
What is GA?
Geometric Algebra is the Clifford Algebra of a vector space over the field of real numbers endowed with a quadratic form. It's an elegant mathematical framework for expressing geometrical ideas and doing computations in fields such as physics, engineering and in computer vision (see Final Report GA for a list of some research applications). It correctly expresses the properties of physical space and one of the main benefits for our project was that it could be extended effortlessly to spaces of arbitrary dimensions.
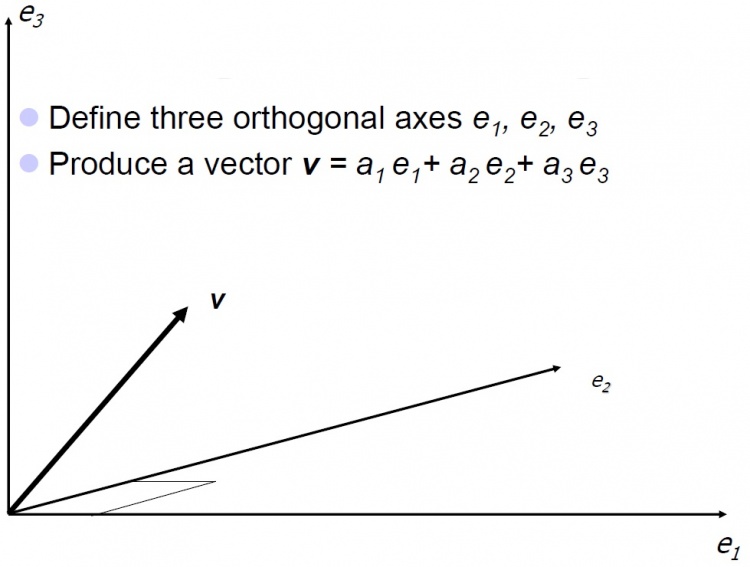
Defining Vectors
How we used it?
Resources
Our Work
See also
- Timing-based key agreement
- Timing Based Encryption: Test Case 1
- Timing Based Encryption: Test Case 2
- Timing Based Encryption: Test Case 3
- Timing Based Encryption: Test Case 4
- Timing Based Encryption: Test Case 5
- Geometric Algebra
- CLUViz Geometric Algebra Animation Software
- Secure communications without key exchange (main page)
- Secure communications without key exchange? 2013 weekly progress
- Proposal Seminar 2013: Secure communications without key exchange?
- Final Seminar 2013: Secure communications without key exchange?
- Semester A Progress Report 2013 - Secure communications without key exchange?
- Semester B Final Report 2013 - Secure communications without key exchange? 2013
- YouTube Videos