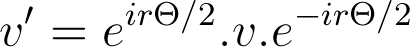Geometric algebra

Rationale

As the main approach inherent in this project involved the use of rotations in Geometric Algebra, we were required to learn the basics of GA with the help of Dr James Chappell. The following description/brief introduction to the fundamental elements of GA is a combination of James' two documents below and numerous other sources. James graciously provided us with his personal powerpoint slides that proved to be an invaluable resource in learning the new materiala as well as a brief worksheet to test your knowledge on GA. Both are provided below in the Useful Resources.

Intro to Clifford's Geometric Algebra & Worksheet #1 in Geometric Algebra

"...it is a good thing to have two ways of looking at a subject, and to admit that there are two ways of looking at it.” James Clerk Maxwell

Geometric Algebra Intro

Geometric Algebra is the Clifford Algebra of a vector space over the field of real numbers endowed with a quadratic form. It's an elegant mathematical framework for expressing geometrical ideas and doing computations in fields such as physics, engineering and in computer vision (see Final Report GA for a list of some research applications). It correctly expresses the properties of physical space and one of the main benefits for our project was that it could be extended effortlessly to spaces of arbitrary dimensions.

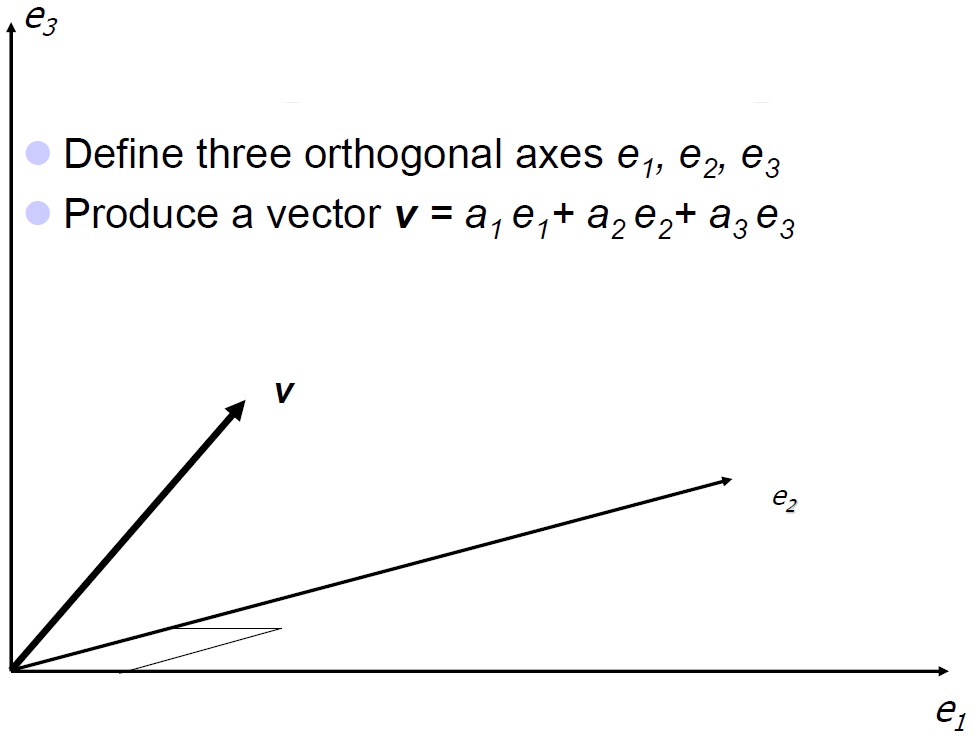
Vectors are defined as shown on the left and are known as Cartesian coordinates, defined by Descartes in 1637. In 1879, Clifford's further described the space by adopting the folllowing-

The 3D space is then simply defined with each plane being defined by the multiple of two of e1, e2 and e3 and the trivector i represents the volume in its entirety. As a result of the anti communicating characteristics, we have Dual Representation of each bivector, by utilising the trivector to give.... e2e3 = ie1, e3e1 = ie2 and e1e2 = ie3.

How we used it?

As mentioned, the dominant method used for our project was rotations with GA, and fortunately enough, the formula for doing said rotations in GA is a very general one. It's shown below and is applicable to rotations of any dimension, whether it be 3D, 4D 5D or even 20D. It's important to note that DeMoivre's theorm applies.

So as mentioned several times throughout the wiki, the original plan for the project was to examine a particular dimension thoroughly, beginging with 3D and either prove or disprove the question of whether or not rotations can be used to achieve secure communication in that dimensions according to the KS cipher. Once this was done, we would move on to a higher dimension and keep doing so until we found a solution or until project closeout- whichever came first.

So in 3D Rotations for an initial message vector m in the form shown below, we apply a Rotation Operator or Rotor R to the message in the shown form, wit a corresponding Reversion Operator applied to opposite side of the message vector as shown.

This gives us the final message vector of the form:

Now as mentioned, we started to explore the 3D rotations to circumvent the vulnerability of 2-dimensional rotations, as given the initial and final rotated message vector in 3D it would not be possible for an eavesdropper to simultaneously deduce the rotation axis and rotation angle, as only the plane of possible rotation axes can be found, and hence it appears to be secure against and eavesdropper. Which as depicted in the image above, the v in the rotation operator R represents the rotation axis around which the rotation occurs and Theta the clockwise rotation angle.

So given 2 rotation operators selected independently by Alice and Bob, let’s say Ra and Rb, each with a unique rotation axis and rotation angle, we have the encryption process shown on the screen to give our final message vector. Where the most inner 2 Rotors around our initial message vector define the original encryption by Alice, the next two the encryption of Bob, and then the 2 on the far left and far right act as the decryption process of both Alice and Bob. However, as we know from the Final Report in order for this process to work we require Ra and Rb to commute, that is we needed RaRb to equal RbRa.

However as we can see through the application of Demoivres theorem, this breaks down to the form shown below, which implies that the cross product of the 2 rotation axes must be 0, and hence the 2 rotation axes of Alice and Bob must be parallel. However in order for Alice and Bob to use parallel Rotation Axes, a preferred direction would need to be communicated beforehand, however this would make the process vulnerable and goes against the premise of the double padlock protocol.

For a much more detailed explanation of the proof for 3D and the difficulties that arose in 4D, please read the Final Report.

Useful Resources

• Intro to Clifford's Geometric Algebra
• Worksheet #1 in Geometric Algebra

Another key document was Geometric Algebra: A natural representation of three-space,by James M. Chappell, Derek Abbott and Azhar Iqbal.

See also

• Timing-based key agreement
• Timing Based Encryption: Test Case 1
• Timing Based Encryption: Test Case 2
• Timing Based Encryption: Test Case 3
• Timing Based Encryption: Test Case 4
• Timing Based Encryption: Test Case 5
• Geometric Algebra
• CLUViz Geometric Algebra Animation Software

• Secure communications without key exchange (main page)
• Secure communications without key exchange? 2013 weekly progress
• Proposal Seminar 2013: Secure communications without key exchange?
• Final Seminar 2013: Secure communications without key exchange?
• Semester A Progress Report 2013 - Secure communications without key exchange?
• Semester B Final Report 2013 - Secure communications without key exchange? 2013
• YouTube Videos