Cipher Cross-off List

Purpose

Previous studies into the Tamam Shud case have concluded that the mysterious code left behind is not just random letters; it is in fact a code. This raises the question: What code was used in encrypting this code? This page is aimed at addressing this question. The Cipher Cross-off list is a place where cipher schemes are listed that have been identified as potentially being used in creating the Somerton Man's code. As part of our project, we will be methodically investigating many of these listed ciphers to see if we can rule them out as being used in the encryption of the code.

Cipher Cross-off List

• Anagram/Transposition Cipher
• Initial letters of a sentence
• Initial letters of an unordered list
• Rail Fence Cipher
• Random Sequence of letters
• Number-Based Ciphers
  • Rotary Telephone Dial Cipher
• Index of Coincidence findings

Substitution Ciphers

• Baconian Cipher
• Beaufort Cipher
• Bifid Cipher
• Dvorak Encoding
• Flat Frequency Ciphers
• Four-square Cipher
• Gronsfeld Cipher
• Hill Cipher
• Keyword Cipher
• Nihilist Cipher
• One Time Pad
• Playfair Cipher
• Playfair Cipher (Double)
• Porta Cipher
• Trifid Cipher
• Two-square Cipher
• Vigenere Cipher

First Order Substitution Ciphers

• Affine Cipher
• Alphabet Reversal Cipher
• Book Cipher
• Homophonic Substitution Ciphers
• Null Cipher
• Pigpen Cipher
• Shift Cipher
• Templar Cipher
• Trithemius Cipher

Stream Ciphers

• Auto-Key Cipher

Substitution and Transposition Ciphers

• ADFGVX Cipher
• VIC Cipher

Reasoning

The following section contains the explanations and/or proofs behind the ruled-out ciphers.

Random Sequence of Letters

As part of their work, the students undertaking this project in both 2009 and 2010 conducted surveys of both sober and intoxicated people to see if the letter frequencies obtained were similar to the letter frequencies evident in the Somerton Man's code. Neither of the groups' surveys were consistent with the code and subsequently it was concluded that it is not simply a random bunch of letters. The relevant sections of the previous groups' work can be seen at the following links:

• 2009: The letters are not random
• 2010: The letters are not random

Anagram/Transposition Cipher

By looking at letter frequency plots of various languages against the code, and by identifying other anomalies such as the existence of a 'Q' but no 'U' in the code, the Honours students in 2009 concluded the code did not use a Transposition Cipher alone. The relevant section of their report can be seen here.

ADFGVX Cipher

The ADFGVX Cipher was introduced to public knowledge in March 1918. It was used primarily by the German Army during World War One. The technique used for encryption produces a ciphertext that contains only the English letters A, D, F, G, V and X, hence the name. The ADFGVX Cipher uses transposition and substitution with bipartite fractionation. Given the lengthy methodology used for encryption and decryption, full details have not been provided. Further information can be accessed here.

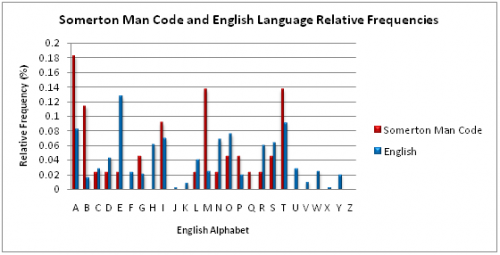
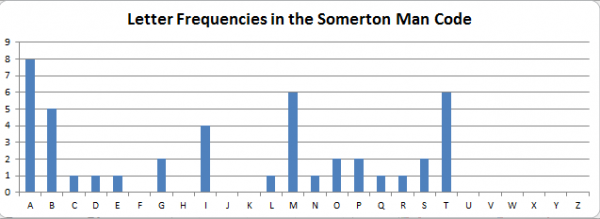
A review of the Somerton Man code showed it contained 16 different English alphabet letters. Thus any cipher methodology that produces a ciphertext with fewer than 16 different letters can be trivially disproven. This includes the ADFGVX Cipher. It was also considered that false letters may have been used to mask the ADFGVX cipher. For this the relative frequency plot for the Somerton Man code was examined. A graph of the relative frequencies of letters in the Somerton Man code compared with the relative English letter frequencies is shown below. There is no evidence that the six letters expected in an ADFGVX ciphertext are more prevalent in the Somerton Man code than in the English language. The ADFGVX Cipher using a weak mask was consequently ruled out of the investigation. Furthermore apart from the letter “A”, the relative frequencies of the six letters is low, three do not even appear. Thus it was also concluded that a strong mask was not used. The ADFGVX was discounted from all further investigation following these results.

Affine Cipher

Like the Shift Cipher, the Affine Cipher is a mono-alphabetic substitution cipher. It is commonly categorised as a block cipher with a length of 1. Each letter of the plaintext is therefore encrypted independently from the other letters.

Encryption method:

[math] e_k(x) = ax + b [/math]

Decryption method:

[math] d_k (y) = a^{-1}(y - b) [/math]

The rules that were examined for encryption and decryption are shown above, where x represents a given plaintext letter and y represents the corresponding ciphertext letter. Given that there was 25 possible values for b within the modulo 26 English Alphabet and 12 possibilities for a, the total number of possible keys for the Affine Cipher was 312. The limitation imposed on a is a consequence of requiring an inverse within the modulo 26 domain.

In 2011, a Java program was written to test all 312 possible key variations. The output from the program has been added to the Cipher Cross-off List wiki page and is available here. The results did not present any understandable text, and as such, the Affine Cipher has been ruled out of any future investigation. The results are available here.

Alphabet Reversal Cipher

The Alphabet Reversal cipher is a substitution cipher where A becomes Z, B becomes Y, C becomes X etc. This leads to the following encoding and decoding key (read in vertical order):

Plaintext Alphabet:   A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Cipher Alphabet   :   Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

Thus, for example, "HELLO" becomes "SVOOL". This cipher was tested on the Tamam Shud code by the 2011 group. A small Java program has been written that takes input from the command line or from a text file and produces output in reversed form. The result of running a file containing the code through the program turns the input of:

MRGOABABD MTBIMPANETP MLIABOAIAQC ITTMTSAMSTGAB

into

NITLZYZYW NGYRNKZMVGK NORZYLZRZJX RGGNGHZNHGTZY

As can be seen, there can be no meaning deciphered from the alphabet-reversed text and thus we can rule out the Alphabet Reversal Cipher as being used in encrypting the Somerton Man's code.

Atbash Cipher

The Atbash Cipher was developed for the Hebrew alphabet, but can be modified to work with the English alphabet. It is identical to the Alphabet Reversal Cipher and is also a special case of the Affine Cipher. Both of these have already been disproven.

Auto-Key Cipher

The auto-key cipher is a stream cipher. Stream ciphers use a different key for every block as opposed to using the same key repeatedly as is the case with block ciphers. In the case of the Auto-Key cipher, the letters of the message are used as the input key stream apart from the first key letter which is normally chosen. The encryption and decryption methodologies that were tested are shown below where k represents the initial key, x_i represents a given plaintext letter and y_i represents the corresponding ciphertext letter.

Encryption method:

[math]e_k(x_i)= x_i + k_i = \begin{cases} x_1 + k & i = 1 \\ x_i + x_{i-1} & i \gt 1 \end{cases}[/math]

Decryption method:

[math]d_k(y_i)= y_i - k_i = \begin{cases} y_1 - k & i = 1 \\ y_i - x_{i-1} & i \gt 1 \end{cases}[/math]

Noticeably only addition is specified within the above formula for encryption however the 2011 project team identified that a variation to the methodology could be present. Specifically in place of the addition, subtraction could have been used. Both were considered in the investigation as well as alternation between addition and subtraction.

Furthermore since the input key stream depends on the message being encoded, the line order of the Somerton Man code is also important. Different line orders yield different message text and uncertainty within the code relating to the crossed out line was a concern in testing the Auto-Key methodology. To ensure thoroughness within the investigation different scenarios were considered. These were:

• The original line order as appears under the Alphabet Reversal Cipher section
• Swapping the order of the second and third lines within the original code. This is to consider the circumstance where a mistake was made when generating the code and the third line is a replacement for the crossed out line.
• Each line separately with the same key used each time.

A Java program was written to test each of the above scenarios with all three possible variations of the decryption formula. Examination of the program’s output file by one of the project team members revealed there was no meaningful English text and as a consequence the Auto-Key Cipher has been ruled out as the technique used to generate the code of the Somerton Man. The output file has been uploaded and is available here.

Baconian Cipher

The Baconian Cipher is a binary-style code using only two letters or formatting variations. The code can also be hidden amongst apparently meaningless text. For example, consider the message "test" encoded using A and B representing binary values.

"test" then becomes BAABB AABAA BAABA BAABB if we use simple letter ordering. This can easily be hidden, for example, Bread can be baked about any ample bastion. Can it be a blessing around a hobby?

For another variation, instead of using A and B, we could use bolded and unbolded letters to represent the binary.

It is clear the Baconian Cipher wasn't used in the Somerton Man Code. Firstly, there is no obvious formatting and secondly the most occuring letters are "A", "T" and "M", which occur 8, 6 and 6 times. This hardly leaves room for much more than a two letter message.

Beaufort Cipher

Invented by Admiral Sir Francis Beaufort (1774 - 1857), the Beaufort Cipher is a polyalphabetic substitution block cipher. The methodology uses different shift ciphers for each letter of the plaintext message, like the Vigenere Cipher. In the same way, a repeated key, usually in the form of a word, specifies the shifts. Instead of the plaintext message forming the basis for the key shift as with the Vigenere Cipher, the Beaufort Cipher uses the key as the basis and the plaintext message as the shift. This gives the Beaufort Cipher the property of reciprocity; the formulas for encryption and decryption are the same. The formulas used in the investigation of the Beaufort Cipher are shown below.

Encryption:

[math] e_k(x_i) = y_i = (k_i-x_i) \mod {n}[/math]

Decryption:

[math] d_k(y_i) = x_i = (k_i-y_i) \mod {n}[/math]

where [math]k = k_0 k_1 k_2 \dots k_d[/math] is the key, [math]x = x_0 \dots x_r[/math] is the plaintext, [math]y = y_0 \dots y_r[/math] is the ciphertext and [math]n[/math] is the number of letters in the alphabet used.

The results of the Index of Coincidence technique indicated feasible block lengths of 3 and 7. For the English alphabet consisting of 26 letters and a block length of three there are (26)^3 = 17576 possible keywords. For a block length of 7 there are over (26)^7 = 8 billion possible keywords; in both cases it was considered as too many keyword combinations to attempt a direct decryption. A frequency analysis of individual letters was conducted as an alternative.

A frequency analysis of the Beaufort Cipher was conducted using block lengths of 3 and 7 as indicated by the Index of Coincidence results. Code words of “NOW” and “ENGLISH” were used in each respective case. 20 independent samples of English the same length as the Somerton Man code were used in the frequency analysis. For consistency both instances used the same English samples. The two graphs below compare the results to the Somerton Man code.

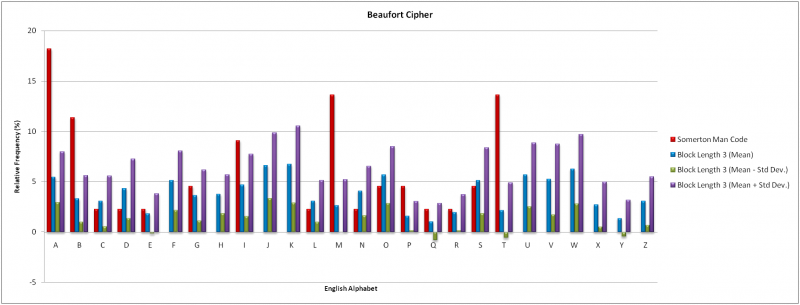
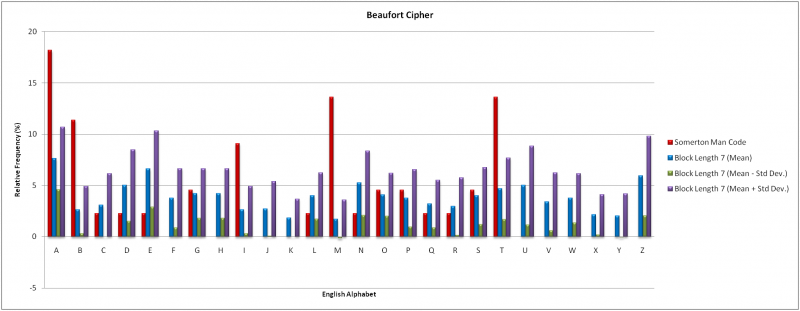
The mean results for both block lengths show a strong correlation. The Beaufort Cipher presents the characteristic of even frequency distribution across all alphabet letters. This is inconsistent with the Somerton Man code. The Somerton Man code has four letters with relative frequencies exceeding 10%. No mean result for a block length of seven shared this result. These results indicate that is unlikely the Beaufort Cipher was used to generate the Somerton Man code. However, given the small amount of data available from the Somerton Man code the results are not conclusive. The Beaufort Cipher has thus been ruled out at this stage but may warrant further investigation if new information about the case or code is revealed.

Bifid Cipher

The Bifid Cipher was first published in 1901. A Polybius square is used with transposition for fractionation encryption. The fractionation that is achieved gives a dependency of each ciphertext character on two plaintext characters, like in the Playfair cipher assessed in 2009. Further information about the Bifid Cipher methodology can be found here.

To test the Bifid Cipher mechanism a known plain text was encoded and the resultant ciphertext was letter frequency analysed and compared to the Somerton Man code. A graph of the relative frequency of each English alphabet letter is shown below. The absence of the letter J in the case of the Bifid Cipher results is in accordance with the encryption methodology where the letters “I” and “J” are represented by the former only.

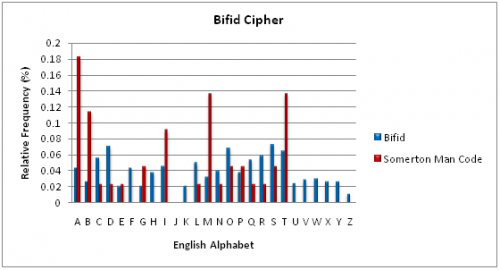
Comparison of the Bifid encryption results with the Somerton Man code shows a weak correlation. The results for the Bifid Cipher case show a distribution between all possible ciphertext letters with a deviation significantly smaller than the Somerton Man code. These results were sufficient to conclude that the Bifid Cipher mechanism had not been used to generate the Somerton Man code. The conclusion is not definitive given the small sample size of the Somerton Man code. An interesting observation is that the letter “J” is absent in both results.

Book Cipher

The Book Cipher requires the sender and recipient of the message to have identical copies of a book or script of writing. The cipher works by replacing words of the plaintext by index numbers corresponding to the word location in the cipher book. For example, if the word "and" appears as the 15th letter in the book, any occurrences of 'and' can be replaced by the number '15' in the ciphertext. Another variation of the book cipher involves coding individual letters via the book, using the index of words starting with the relevant letter. Since the Somerton Man code is made of letters rather than numbers, we can rule out the Book Cipher.

Dvorak Encoding

Dvorak Encoding is a monoalphabetic substitution cipher based on the Dvorak Keyboard, a keyboard layout invented in 1936 with the goal of reducing finger distance travel to increase typing rates. The encoding works by simply typing the plaintext into a Qwerty keyboard using the Dvorak layout. As can be seen from the picture below, this would transform QWERTY to ',.PYF.

Decrypting Dvorak Encoding simply involves reversing the previous step - typing the ciphertext into a Dvorak Keyboard using Qwerty layout.

A slight variation on Dvorak Encoding is to type the plaintext into a Dvorak Keyboard using the Qwerty layout and decrypt by typing into a Qwerty Keyboard using the Dvorak layout. Both methods have been tested on the Somerton Man code, both producing no logical output (shown below). Thus Dvorak Encoding has been crossed off the list.

Plain Dvorak (De)Coding

MPIRAXAXE MYXCMLAB.YL MNCAXRACA'J CYYMYOAMOYIAX

Alternate Dvorak (De)Coding

MOUSANANH MKNGMRALDKR MPGANSAGAXI GKKMK;AM;KUAN

Flat Frequency Ciphers

Flat Frequency distribution ciphers have a flat letter frequency distribution – that is, there is an equal probability for each symbol of the cipher alphabet to occur. The letter frequency plots should be flat. Examples of flat frequency ciphers include:

• One Time Pad - The One Time Pad uses a random key that is the same length of the text to encrypt the message. The randomness and length of the key cause the frequency distribution of the encrypted text to have a flat letter frequency distribution.
• Homophonic Substitution Ciphers - Homophonic Substitution ciphers replace commonly occurring plaintext letters with multiple ciphertext symbols. For example, the letter ‘e’ occurs roughly 13% of the time in English text, thus it could be replaced by 13 different symbols. Through this method, these ciphers also produce a flat response, although they typically have a larger cipher alphabet.

The Somerton Man code letter distribution does not appear flat at all… So lets prove it!

Hypothesis: The Somerton Man code was produced using a flat frequency cipher. How can we test this? The code has 44 letters. Nearly one fifth (8) of these are the same letter (‘A’). But for a flat frequency distribution, the probability of a letter occurring at each point is approx. 1/26.

• Null Hypothesis – H_0: The occurrence of eight ‘A’s in the code is consistent with a flat frequency code.
• Alternate Hypothesis – H_a: The occurrence of at least eight ‘A’s in the code is inconsistent with the use of a flat frequency code.

Probability of ‘A’ occurring for any letter assuming the null hypothesis (flat distribution) is:

[math]Pr(A)= {1 \over 26} [/math]

This assumes the entire English alphabet is used.

Using binomial distribution, the probability of n occurrences of the letter ‘A’ in 44 letters in a flat frequency distribution ciphertext is given by:

[math]P(A=n)= C_n^{44} \left({1\over26}\right)^n \left({25\over26}\right)^{(44-n)}[/math]

Therefore the probability of no ‘A’s occurring in 44 letters is:

[math]P(A=0)=C_0^{44} \left({1\over26}\right)^44=0.1780[/math]

The probability of 1,2,…,8 ‘A’s occurring in 44 letters is given by:

[math]P(A=1)=C_1^{44} \left({1\over26}\right)^1 \left({25\over26}\right)^{43}=0.3130[/math] [math]P(A=2)=C_2^{44} \left({1\over26}\right)^2 \left({25\over26}\right)^{42}=0.2695[/math] [math]P(A=3)=C_3^{44} \left({1\over26}\right)^3 \left({25\over26}\right)^{41}=0.1509[/math] [math]P(A=4)=C_4^{44} \left({1\over26}\right)^4 \left({25\over26}\right)^{40}=0.0619[/math] [math]P(A=5)=C_5^{44} \left({1\over26}\right)^5 \left({25\over26}\right)^{39}=0.0198[/math] [math]P(A=6)=C_6^{44} \left({1\over26}\right)^6 \left({25\over26}\right)^{38}=0.00515[/math] [math]P(A=7)=C_7^{44} \left({1\over26}\right)^7 \left({25\over26}\right)^{37}=0.00112[/math]

We can use this to calculate the probability of eight or more ‘A’s occurring. [math]P(A\ge8)=1-P(A\le7)=1-P(A=0)-P(A=1)-P(A=2)-P(A=3)-P(A=4)-P(A=5)-P(A=6)-P(A=7)[/math]
[math]P(A\ge8)=1-0.1780-0.3130-0.2695-0.1509-0.0619-0.0198-0.00515-0.00112[/math]
[math]P(A\ge8)=1-0.99975=0.00025[/math]

Testing at the 5% significance level, since 0.00025 << 0.05, we can safely reject the null hypothesis and accept the alternate hypothesis that it is likely that a flat frequency encoding technique has NOT been used in creating the Somerton Man code.
We can extend this to other letters. Realistically, it could have been any of the 26 letters occurring 8 times. To account for this, we can times the test statistic by 26.

[math]t_{new}=26\times0.00025=0.0065[/math]

As 0.0065 << 0.05, we can again reject the null hypothesis at the 5% significance level and conclude that a flat frequency cipher was not used to encode the Somerton Man Code.

This rules out both the One Time Pad and any Homophonic Substitution cipher.

Four-square Cipher

The Four-square Cipher is similar to the Playfair Cipher and the Two-square Cipher in that it is a digraph cipher - it encrypts letters in pairs. This means that the output code should occur in even numbers. In the case of the Somerton Man's code, the lines consist of 9, 11, 11 and 13 letters - no even numbers. This would indicate that a simple digraph encryption technique, including the Four-square Cipher has not been used. Unless of course, null (padding) characters have been added to the end of each line...

Gronsfeld Cipher

The Gronsfeld Cipher is a variation of the Vigenere Cipher. Like the latter it is a polyalphabetic substitution block cipher. The encryption and decryption methodologies, shown below, are the same as the Vigenere Cipher.

Encryption:

[math] e_k(x_i) = y_i = (x_i+k_i) \mod {n}[/math]

Decryption:

[math] d_k(y_i) = x_i = (y_i-k_i) \mod {n}[/math]

where [math]k = k_0 k_1 k_2 \dots k_d[/math] is the key, [math]x = x_0 \dots x_r[/math] is the plaintext, [math]y = y_0 \dots y_r[/math] is the ciphertext and [math]n[/math] is the number of letters in the alphabet.

The available keys differentiate the Gronsfeld Cipher from the Vigenere Cipher. The Vigenere Cipher accepts a key specified by letters, thus for one letter in the plaintext permits any shift within modulo 26 for the English alphabet. The Gronsfeld Cipher uses a numerical key that represents a series of single digit shifts; for one letter in the plaintext any shift within modulo 10 is permissible independent of language. The ciphertexts available with the Gronsfeld Cipher are therefore a subset of those attainable with the Vigenere Cipher.

All results obtained in the investigation of the Vigenere Cipher are applicable to the Gronsfeld Cipher. A convention of the Gronsfeld Cipher is to use keys without repeated digits. The two keywords of “NOW” and “ENGLISH” used in the Vigenere Cipher investigation satisfy this convention. Both keywords do contain shifts beyond the modulo 10 boundary of the Gronsfeld Cipher however the common methodology with the Vigenere Cipher imposes the same letter frequency profile. Thus no further investigation was required for the Gronsfeld Cipher.

Hill Cipher

The Hill Cipher was invented by Lester S. Hill in 1929. It is a polygraphic polyalphabetic substitution cipher based on linear algebra. The encryption and decryption methodologies that were tested are defined by the formulas shown below. Encryption method:

[math] e_A(x) = xA [/math]

Decryption method:

[math] d_A(x) = yA^{-1} [/math]

The matrix A is required to be invertible within the alphabet used, for English this is modulo 26.

Given it is a block cipher the results of the Index of Coincidence method were extremely helpful for analysis of the Hill Cipher. The 2011 investigation concluded that since the code was generated by hand, encryption key matrix sizes of 2x2 and 3x3 were most practically feasible. However reflection on the findings of the Index of Coincidence Method showed the most likely block lengths were 3 and 7. A block length of two, corresponding to a 2x2 encryption key matrix, was deemed unlikely. Furthermore a block length of two would yield a digraph cipher, meaning the ciphertext was generated in pairs. The Somerton Man code contains lines consisting of 9, 11, 11 and 13 letters. There are no even numbers of letters on any line. From this and the results of the Index of Coincidence method, it was concluded the Hill Cipher using a dimension two encryption key could be ruled out as the source of the Somerton Man code. As only the first of four lines was a multiple of three, a Hill Cipher using a dimension three encryption key was also ruled out.

Homophonic Substitution Ciphers

Homophonic Substitution Ciphers are substitution ciphers that use multiple symbols for more common letters (such as 'e') in an attempt to confuse cryptanalysts trying to crack the code through frequency analysis. For example, if 'e's occur 14% of the time, use 14 different symbols for 'e' during the encryption process. There are two reasons we can rule out a homophonic substitution cipher. Firstly, this sort of cipher requires a cipher alphabet of much greater size than the plaintext alphabet. From what we can see, the Somerton Man code simply uses the English alphabet. Secondly, homophonic substitution ciphers theoretically produce flat frequency distributions. The Somerton Man Code's letter frequency is clearly not flat, as can be seen below.

The statistical proof showing that the code's letter distribution is not flat can be seen in the Flat Frequency Cipher section.

Index of Coincidence findings

A block length of size five was used to analyse the Vigenere Cipher in 2009. The investigation in 2011 attempted to identify if there were any possible block lengths besides size five for the Somerton Man code. As the results to follow consider the block length statistically, the findings are applicable to any cipher mechanism using a block-based structure.

The technique used to identify possible block lengths was the Index of Coincidence. Mathematically, it is defined as the probability that any two randomly chosen characters within a text (plaintext or ciphertext) are the same letter.

The formula for calculating the probability for the English alphabet (modulo 26) is shown below where fi denotes the number of occurrences of the i-th letter of the input text alphabet and n represents the number of letters in the message.

[math]I_c(x) = \frac{\displaystyle\sum_{}f_i(f_i - 1)}{n(n - 1)},[/math]

For a random string of text the Index of Coincidence returns Ic(x) = 26(1/26)^2 = 0.038 and for a string of English text, Ic(x) = 0.065. The ciphertext was divided into blocks of different length, the indices of coincidence calculated and compared to the English case. Strong correlation between the index of coincidence of every block and the English case above indicated the number of blocks as a possible block length.

The Index of Coincidence technique required the divided blocks of ciphertext were equivalent to writing the ciphertext as columns in a matrix of m rows, where m is the number of blocks. The example below summarises how this was done.

Ciphertext: “HIDDEN SECRET MESSAGE”
Block number: 3

Block 1: H D S R M S E
Block 2: I E E E E A
Block 3: D N C T S G

For the Somerton Man code of 44 letters, the Index of Coincidence technique was used to test all block lengths up to and including length 22. A length of 22 corresponded to blocks of two letters, the minimum possible when assessing two characters as the same letter.

A Java program was written to automate the testing and the program and results are available here. Comparing each index of coincidence with the English case above shows if a block-based cipher was used to generate the Somerton Man code, lengths of 3 and 7 were most likely used.

Keyword Cipher

The Keyword Cipher is a simple mono-alphabetic substitution cipher, created by listing a keyword under the plaintext alphabet then filling in the remaining letters. Any repeated letters in the keyword are ignored. For example, using the keyword SOMERTON, the translation from the plaintext alphabet to the cipher alphabet becomes:

Plaintext Alphabet:   A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Cipher Alphabet   :   S O M E R T N A B C D F G H I J K L P Q U V W X Y Z

There is a very good possibility that a Keyword Cipher was used to generate the Somerton Man's code. The reasoning behind this viewpoint follows.

Firstly, note how towards the end of the alphabets above, the Cipher Alphabet and the Plaintext form become very similar due to the nature of the keyword encoding. With this in mind, examining the following letter frequency plot of the Code letter frequencies against English letter frequencies has a fascinating result - towards the end of the alphabet (S,T,U,V,W,X,Y,Z) there is good correllation between the code and English letter frequencies. However at the start of the alphabet there are vast discrepancies.

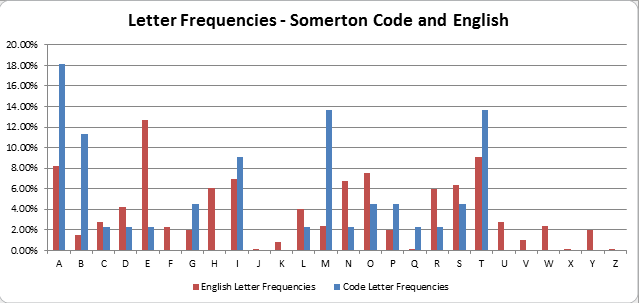
This result is consistent with a Keyword-encoded cipher, where the keyword at the start of the cipher alphabet makes for significant displacements in letter substitutions, whereas, as the keyword ends and the remainder of the alphabet fills in to complete the cipher alphabet, the letter substitution displacements become closer and closer together, as evidenced by the example Plaintext and Cipher alphabets shown above.

While the letter frequency plots show there is a chance that the code was formed using the Keyword Cipher, it is difficult to confirm or rule it out. This is due to the limited number of letters in the Somerton Man's code we have to work with. Usually we would perform frequency analysis on the code to determine the keyword, however with only 44 letters to work with, frequency analysis will not be accurate.

If the Keyword Cipher was used in encrypting the code, we can make guesses as to what sort of keywords could have been used. The effect of a keyword in transforming the plaintext alphabet to the ciphertext alphabet is:

• Create a random sequence at the beginning (according to the keyword) - e.g. plaintext A,B,C,D,E,F,G --> ciphertext K,E,Y,W,O,R,D
• Shuffle the rest of the alphabet along at a decreasing rate as keyword letters are filtered out.

From this, we can guess that the keyword would contain no letters later than "T", as the following letters in the alphabet have a good frequency match to normal English frequencies - i.e. we want the shuffling along to be finished. Another guess we can make is that either the keyword is 4 letters long or the fifth letter is an 'A'. Either of these circumstances would cause ciphertext 'A' to line up with plaintext 'E', converting the code-frequency dominant A's into English frequency dominant plaintext E's.

Nihilist Cipher

The Nihilist Cipher utilises a Polybius square with a keyword to provide a mixed alphabet. The square is used to convert each plaintext letter as well as a second keyword different to the first, into a two digit number. The ciphertext is obtained by adding the plaintext letter values and the corresponding keyword letter values. The keyword numbers are repeated as required. An example of the Nihilist Cipher methodology can be seen here.

As the Nihilist Cipher mechanism produces a ciphertext consisting of only numerical values, use for the Somerton Man code can be trivially disproven given that the Somerton Man code is formed from only letters.

Null Cipher

The mysterious code found marked in the back of the Rubaiyat.

The Null Cipher is a form of Steganography - which involves hiding the real message rather than making it unintelligible as with substitution and transposition ciphers. In the Null Cipher, the plaintext of the message is disguised by blending it in with a large amount of 'null' or non-cipher text. For example, we can hide the message Hidden Words in the initial letters of Horrors in Derek's den entice naive wanderers. Ominous remains describe sacrifices.

Usually Null Cipher-encoded ciphertext is in easily understandable text so that it is not evident there is a hidden message inside and also long given the null letters padding out the text. The Somerton Man's code is relatively short so it does not appear to be a typical Null Cipher. However there is always a chance there is a small message, for example a place name, encoded in the text. There are many ways a message could be encoded, for example, if we look at the code in the picture to the right, there are several letters with distinctive markings that could form part of the plaintext: 'O' and 'C' in the third line and 'S' and 'S' in the fourth line.

While the Null Cipher cannot be completely ruled out, it is unlikely.

Number-Based Ciphers

Number codes include those such as simple letter-number substitutions and Phone Keypad encryption systems. All number-based ciphers can easily be discounted as the Somerton Man code is formed of letters, with no numbers.

Rotary Telephone Dial Cipher

Given the prevalence of rotary dial telephones in 1948 a cipher was considered that used their faces. A template of a typical rotary dial telephone can be seen to the left showing both the available numbers and corresponding letters. Importantly, the letter “Q” is absent. The code of the Somerton Man contains an instance of the letter “Q”, thus the face of a rotary dial telephone could not have been used as an encryption mechanism. As a consequence any cipher using the face of a rotary dial telephone has been disproven and will not be further investigated.

One Time Pad

The One-Time pad has been investigated by the 2009 group. They experimented using the Rubaiyat of Omar Khayyam (which is closely linked with the case) and the King James Bible (common at the time) and found no key to de-ciphering the code. Their conclusions can be seen here: 2009 One-Time Pad Conclusion

The One Time Pad has been re-examined in 2011.

The One Time Pad uses a random key that is the same length of the text to encrypt the message. The randomness and length of the key cause the frequency distribution of the encrypted text to have a flat letter frequency distribution.

It has been ruled out as being used based on the statistics indicating the Somerton Man's Code does not have a flat letter frequency distribution. The proof for this can be seen in the Flat Frequency Cipher section.

In 2012, the logic behind ruling out the One Time Pad was re-examined, and it was concluded that the flat frequency response relies on the assumption that the pad used is random. This may not be the case, for example if the pad was a section of a book. Since there is an almost infinite number of possible keys it is impossible to definitively rule out the One Time Pad as a possible cipher.

Pigpen Cipher

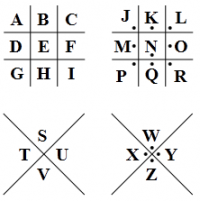
The Pigpen Cipher is a simple geometric substitution cipher, known for its use by the Freemasons in the 1700s to keep their records secret. The cipher substitutes letters according to the diagram to the right. The resulting cipher is formed of geometric parts of the structure corresponding to the relevant letter - thus the cipher is formed of partial squares, triangles and dots rather than letters. The Somerton Man code is formed of letters and thus we can rule it out.

Playfair Cipher

The 2009 students concluded that the cipher used was not likely to be the Playfair Cipher based on an empirical test they performed. Their conclusion can be seen here: 2009 Playfair Cipher Conclusion

The Playfair Cipher has also been re-examined in 2011. The cipher was popularised by Baron Playfair of St Andrews, but it was actually invented in 1854 by Sir Charles Wheatstone; a pioneer of telegraph and inventor of the Wheatstone Bridge.

The Playfair Cipher is a digraph substitution cipher in which pairs of plaintext are replaced by pairs of ciphertext letters. The cipher involves the creation a 5x5 square (I and J share the same reference) using a keyword. For example, using the keyword Playfair we could create the following square:

P L A Y F
I R B C D
E G H K M
N O Q S T
U V W X Z

For each pair of letters, a rectangle is traced out in the Playfair square, and the plaintext pair is replaced by the letters in the alternate corners of the rectange. For example, if we encoded TH (as shown below) we would return the coded pair QM.

P L A Y F
I R B C D
E G|H K M|
N O|Q S T|
U V W X Z

There are three special cases that must be considered -

• if the plaintext pair is the same letter repeated, an X is usually inserted between them
• if the plaintext pair share the same row, the letters are replaced by those immediately to the right
• if the plaintext pair share the same column, they are replaced by those directly below

Cracking the Playfair Cipher is easiest done by Frequency Analysis - analyse which digraphs occur most commonly in English (or the chosen language) and compare this to the distribution of digraphs in the ciphertext. Unfortunately, digraph frequency analysis requires a large amount of data to compare. The 22 pairs available in the Somerton Man's code do not provide sufficient data for this (although there are three "AB" pairs). This means we must try to analyse it in different ways.

There are two factors that point to the Playfair Cipher not being used in creating the Somerton Man code.

• The cipher tends to have a flattening effect on on the frequency distribution of individual letters. The Somerton Man code has three letters (A, M, T) with frequencies well above 10%. 20 samples (the same size as the code) of English text were taken and encrypted. Of these, just 2 encrypted samples (i.e. 1/10) had three letters with 10% or greater frequencies. The other samples all had 0, 1 or 2 letters above the 10% mark. While this doesn't rule it out, it does make the use of the Playfair Cipher more unlikely.
• Due to the nature of the cipher, there are never encrypted double letter pairs - i.e. you never see "EE" or "HH" paired letters. Looking at the pairing of the Somerton Man code, we see a "TT" towards the end. This would appear to rule out the Playfair Cipher as being used in forming the code.

MR GO AB AB DM TB IM PA NE TP ML IA BO AI AQ CI TT MT SA MS TG AB

Playfair Cipher (Double)

The Double Playfair Cipher is an extension of the previously examined Playfair Cipher. The Double Playfair Cipher uses the same digraph substitution methodology with two 5x5 squares in place of one. It is orthodox to use a different keyword for each square. The methodology that was investigated is extensive and is available here.

The use of two squares within the encryption methodology has resolved the absence of double letter pairs in ciphertexts. Thus unlike the Playfair cipher the instance of the letter pair “TT” in the code could not be used to disprove the use of the cipher. Historically a frequency analysis of digraphs is used. This requires a significant source of data which is not available with the 22 letter pairs available in the Somerton Man code. As an alternative a frequency analysis of individual letters was conducted.

The frequency analysis considered block lengths of 3 and 7 as a reflection of the results from the Index of Coincidence testing. 20 independent samples of English text equal in length to the Somerton Man code were used with the keywords “NOW” and “ENGLISH”. The results of both cases are compared to the Somerton Man code in the graphs below.

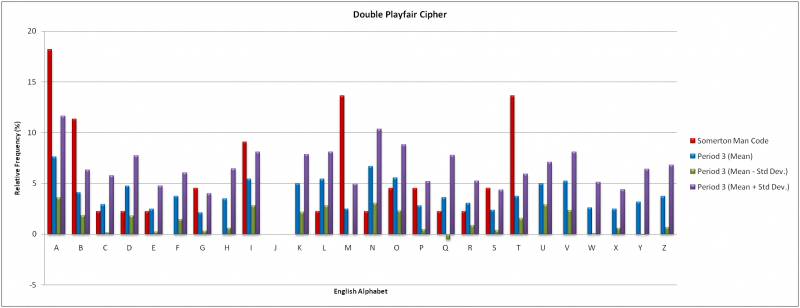
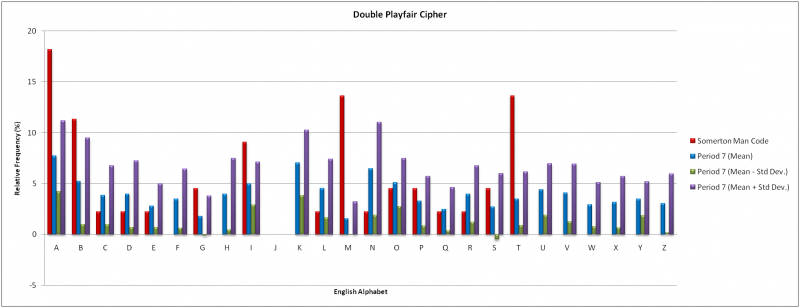
There was no correlation between the mean results for a block length of three and the Somerton Man code. Only the letters ‘C’, ‘E’, ‘O’ and ‘R’ were comparable. The mean results for a block length of seven were consistent with those of a block length of three; with the same dissimilarities to the Somerton Man code. In both cases the mean results for the letter ‘I’ which includes all instances of the letter ‘J’, were inconsistent with the Somerton Man code. The omission of the letter ‘J’ from both encryption squares and the subsequent absence from all ciphertexts interestingly is consistent with the Somerton Man code.

It is unlikely that the Double Playfair Cipher was used to produce the Somerton Man code however this conclusion relies on the assumption that the true letter frequencies are accurately reflected in the 44 letters of the code. If a larger sample becomes available further investigation is warranted.

Porta Cipher

The Porta Cipher was invented in 1565 by Giovanni Battista Della Porta. It is a polyalphabetic substitution block cipher with encryption and decryption performed using the table shown below. There are thirteen possible shift ciphers for each letter of the plaintext message. The shift is specified by the current letter of a repeated key, traditionally in the form of a word.

The results of the Index of Coincidence technique indicated feasible block lengths of 3 and 7. For a block length of three there are (13)^3 = 2197 possible keywords. A block length of 7 has over (13)^7 = 62.7 million possible keywords; in both cases a direct decryption was deemed infeasible. As an alternative a frequency analysis of individual letters was conducted.

In accordance with the results from the Index of Coincidence testing, the frequency analysis of the Porta Cipher considered block lengths of 3 and 7. Code words of “NOW” and “ENGLISH” were used with 20 independent samples of English the same length as the Somerton Man code. The two sets of results are compared to the Somerton Man code in the graphs below.

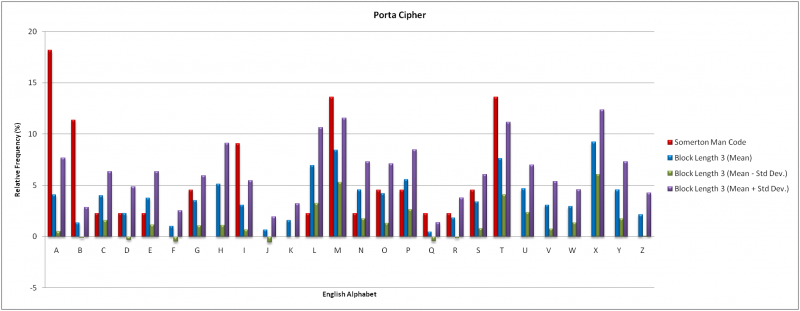
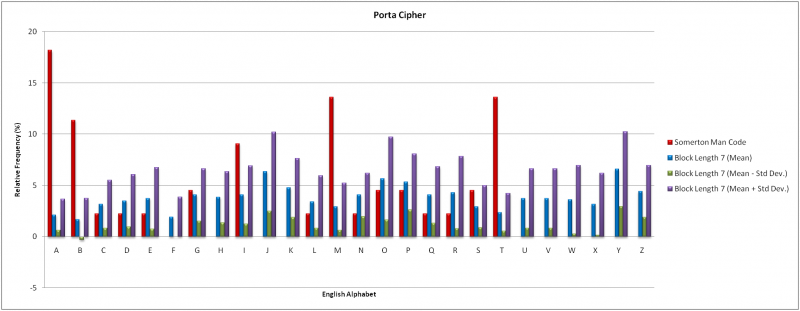
The mean results for a block length of three shows of the 16 letters in the Somerton Man code only letters ‘D’, ‘O’, ‘P’ and ‘R’ had consistent frequencies. There were also a several letters absent from the code that had high occurrences in the mean results. For a block length of seven the characteristic of even frequency distribution across all alphabet letters is exhibited. Only letters ‘J’, ‘O’, ‘P’ and ‘Y’ showed a disproportionally high occurrence for the mean results. This is inconsistent with the Somerton Man code. It is thus unlikely that the Porta Cipher was used to generate the Somerton Man code. The cipher has been ruled out at this stage however infers the 44 letters of the Somerton Man code is a sufficient data sample. Further investigation is warranted if a larger sample becomes available.

Rail Fence Cipher

The Rail Fence Cipher (or zigzag cipher) was identified as a possibility because of the four distinct lines indicating it could be a 4-rail cipher. A Rail Fence Cipher involves writing out the unencrypted message in a zigzag and then reading it in rows to form the encrypted version. For example, take "Rail Fence Cipher" in a 3-rail cipher:

R   F   E   H    
 A L E C C P E   
  I   N   I   R  

The encrypted form is therefore: RFEH ALECCPE INIR.

We can discount the Rail Fence Cipher as being used in the Tamam Shud code for several reasons. Firstly, it is simply a transposition cipher and previous studies have shown the letter frequency plot is not consistent with a transposition. The presence of a 'Q' in the code without a 'U' also indicates it is unlikely to be a transposition cipher. The final indicator comes from testing the code itself:

   M     R     G     O     A     B     A     B     D 
  M T   B I   M P   A N   E T   P     
 M   L I   A B   O A   I A   Q C      
I     T     T     M     T     S     A     M     S     T     G     A     B

As we can see, the zigzags do not form recognisable words, and there are extra letters overflowing from the top and bottom lines.

Shift Cipher

The shift cipher is a mono-alphabetic cipher and in the most general description is literally a substitution cipher. Each letter is shifted by the same amount within the alphabet that is used and the modulo operator ensures any shift remains within the alphabet. One implementation of the shift cipher is famously known as the Caesar Cipher, but while the Caesar Cipher only uses one value for the key the following examination explores all available options. The encryption and decryption methodologies are shown below where x represents a given plaintext letter, y represents the corresponding ciphertext letter and k is the key, which is restricted by the size of the alphabet used.

Encryption method:

[math]e_k(x) = y = x + k [/math]

Decryption method:

[math]d_k(y) = x = y - k [/math]

The shift cipher has been tested in 2011 with the Java code that was used cycling through all 25 key options within the English Alphabet, reduced by one to remove the zero shift case. The results have been uploaded and can be found here. Since the results show no understandable text, the shift cipher has been removed from future project investigations.

It is worth noting that the results of this test will be confirmed with the future implementation of a testing procedure for the Affine Cipher corresponding to the case of a = 1.

Templar Cipher

The Templar Cipher is a variation of the Pigpen Cipher and was used by the Knights Templar some time after their founding in 1118. Letters of the plaintext are substituted with symbols in accordance with the diagram below. The letter “J” is encoded with the same symbol as the letter “I”. As ciphertexts generated using the Templar Cipher consist of only symbols and the Somerton Man code consists of only letters, the Templar Cipher can be removed from further investigation.

Trifid Cipher

The Trifid Cipher was invented in 1901 following publication of the Bifid Cipher. It extends the Bifid Cipher into a third dimension which consequently achieves fractionation that sees each ciphertext character dependent on three plaintext characters. Further information about the Trifid Cipher and example of the encryption methodology can be found here. As the Trifid Cipher requires 27 ciphertext letters, the full-stop was used for the additional character like in the reference material.

Since the Somerton Man code did not contain any characters beyond the traditional English Alphabet, the Trifid Cipher mechanism could not be trivially discounted. Testing therefore followed the same procedure as the Bifid Cipher; a known plaintext was encoded and the resultant ciphertext was letter frequency analysed and compared to the Somerton Man code. The relative frequency of each English Alphabet letter is shown in the graph below, with the “Dot” letter representing the 27th ciphertext character.

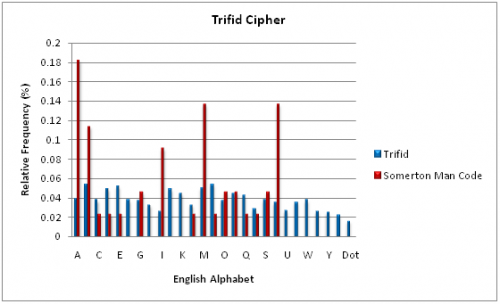
The Trifid Cipher shows an approximately even distribution across all ciphertext letters. The Somerton Man code in comparison is sporadic, with the proportion of letters “A”, “B”, “M” and “T” much larger. From these results it was decided that the Trifid Cipher had not been used to generate the Somerton Man code however as was the case with the Bifid Cipher, the small sample size of the Somerton Man code prevents a definitive conclusion being reached.

Trithemius Cipher

The Trithemius Cipher is a polyalphabetic substitution cipher invented by Johannes Trithemius in the 15th century. It uses the Trithemius table which is shown below and consists of the 26 letters of the English alphabet forming the first line followed by 25 rows of the same letters shifted once to left each time (25 different shift ciphers).

Encryption of the plaintext message is achieved by using the top line as the plaintext guide and selecting a letter below from the same column. The first plaintext letter uses the first row of the table, the second letter uses the second row of the table and so on. At the 27th letter operation returns to the first line if needed. An example is the message “THIS IS SECRET”, which would be encoded as: “TIKV MX YLKAOE”.

The Trithemius Cipher has been tested with java code that deciphers the Somerton Man code directly. The results contained no understandable plaintext thus the Trithemius Cipher has been ruled out of further investigations.

Two-square Cipher

The Two-square Cipher is similar to the Playfair Cipher in that it is a digraph cipher - it encrypts letters in pairs. This means that the output code should occur in even numbers. In the case of the Somerton Man's code, the lines consist of 9, 11, 11 and 13 letters - no even numbers. This would indicate that a simple digraph encryption technique such as the Two-square Cipher has not been used.

The Two-square Cipher is also known as the Double Playfair Cipher. Thus the reasoning for the Double Playfair is also relevant here.

VIC Cipher

The VIC Cipher was a cipher scheme issued by the Soviet Union. The version that was examined in the following investigation was the one adapted to the English language thus coinciding with the Somerton Man code. Further information about implementation of the VIC Cipher is available here. Use of the VIC Cipher to generate the Somerton Man code can be trivially disproved as its formula outputs ciphertext consisting only of numerical blocks of length five while the Somerton Man code contains only letters.

For completeness a conversion between numbers and letters was considered. Two cases were examined. The first that there was a two digit number representing each letter in the code and the second using the conventional representation of Z₂₆ with A = 0, B = 1, etc. Both instances failed to produce a numerical representation that was a factor of five which would be inherent in the use of the VIC Cipher system. The possibility that dummy variables could have been used to pad the size were dismissed as too remote and it was decided no change would be made to the original conclusion that the VIC Cipher was not used.

As mentioned above the VIC Cipher scheme that was investigated was the version adapted to the English language thus there is an opportunity for future exploration of alternative languages.

Vigenere Cipher

Investigation of the Vigenere Cipher scheme in 2009 ruled that it had not been used to produce the code of the Somerton Man. Upon reviewing the findings, the 2011 project team concluded that further enquiries needed to be pursued before the Vigenere Cipher could be dismissed.

The Vigenere Cipher is a polyalphabetic substitution block cipher. The methodology uses a shift for each letter of the plaintext message which is specified by a repeated key, traditionally in the form of a word. The formulas used in the investigation of the Vigenere Cipher are shown below.

Encryption:

[math] e_k(x_i) = y_i = (x_i+k_i) \mod {n}[/math]

Decryption:

[math] d_k(y_i) = x_i = (y_i-k_i) \mod {n}[/math]

where [math]k = k_0 k_1 k_2 \dots k_d[/math] is the key, [math]x = x_0 \dots x_r[/math] is the plaintext, [math]y = y_0 \dots y_r[/math] is the ciphertext and [math]n[/math] is the number of letters in the alphabet used.

The Index of Coincidence findings indicated likely block lengths of 3 and 7. The Vigenere Cipher has (26)^3 = 17576 possible keywords for a block length of three and (26)^7 = 8 billion possible keywords; an infeasible amount in both cases to use direct decryption. As an alternative a frequency analysis of individual letters was used. 20 independent samples of English text equal in length to the Somerton Man code were used with the keywords “NOW” and “ENGLISH”. The results of both cases are compared to the Somerton Man code in the graphs below.

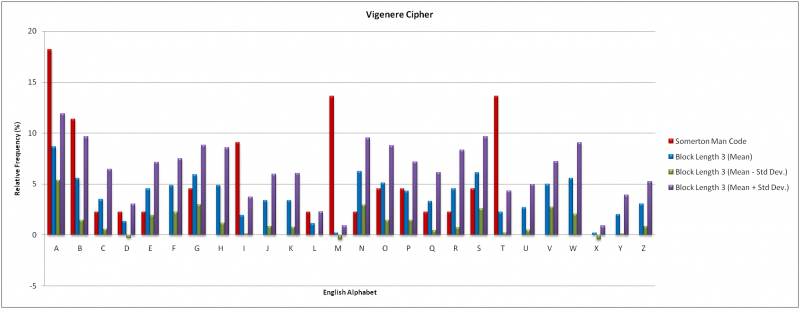
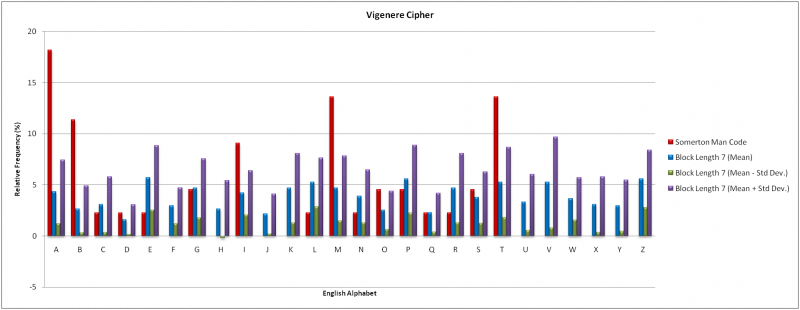
The mean results for a block length of three showed minimal consistency with the Somerton Man code. Letters ‘O’, ‘P’, ‘G’ and ‘S’ had similar frequencies however the four letters in the code with frequencies exceeding 10%, particularly the letter ‘M’ , did not compare favourably. There were also several letters absent from the code that had high occurrences in the mean results. For a block length of seven the mean results exhibited strong correlation towards even frequency distribution across all alphabet letters. This is inconsistent with the Somerton Man code.

It is unlikely that the Vigenere Cipher was used to produce the Somerton Man code however this conclusion infers that the 44 letter code accurately represents the letter distribution of a significantly larger sample. Further investigation is warranted if such a sample is obtained.

See also

• Final Report 2011
• Stage 1 Design Document 2011
• Stage 2 Progress Report 2011
• 2011 CipherGUI File:Cipher GUI.rar
• 2011 YouTube Project Video
• Timeline of the Taman Shud Case
• List of people connected to the Taman Shud Case
• List of facts on the Taman Shud Case that are often misreported
• List of facts we do know about the Somerton Man
• The Taman Shud Case Coronial Inquest
• Letter frequency plots
• Structural Features of the Code
• Markov models
• Primary source material on the Taman Shud Case
• Secondary source material on the Taman Shud Case
• Transition probabilities from selected texts
• Listed poems from The Rubaiyat of Omar Khayyam
• Using the Rubaiyat of Omar Khayyam as a one-time pad
• Using the King James Bible as a one-time pad
• Using the Revised Standard Edition Bible as a one-time pad
• Transitions within words

References and useful resources

If you find any useful external links, list them here:

• The taman shud case
• Edward Fitzgerald's translation of رباعیات عمر خیام by عمر خیام
• Adelaide Uni Library e-book collection
• Project Gutenburg e-books
• Foreign language e-books
• UN Declaration of Human Rights - different languages
• Statistical debunking of the 'Bible code'
• One time pads
• Analysis of criminal codes and ciphers
• Code breaking in law enforcement: A 400-year history
• Evolutionary algorithm for decryption of monoalphabetic homophonic substitution ciphers encoded as constraint satisfaction problems

Back

• Back to MyUni
• Back to Derek Abbott's homepage
• Back to EEE Department page
• Back to the University of Adelaide homepage